순차탐색알고리즘
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법
- 주로, 정렬되지 않는 리스트에서 데이터를 하나씩 차례대로 확인하는 방법
- 리스트 내에 데이터가 아무리 많아도 시간만 충분하다면 항상 원하는 원소(데이터)를 찾을 수 있다는 장점
- 리스트에 특정 원소가 있는 지 체크할 경우, 리스트에서 특정한 값을 가지는 원소의 개수를 세는 count() 메서드 이용할 경우
#순차 탐색 코드
def sequentail_search(n,target,array):
#각 원소를 하나씩 확인하며
for i in range(n):
#현재의 원소가 찾고자 하는 원소가 동일한 경우
if array[i] == target:
return i+1 #현재의 위치 변환(인덱스는 0부터 시작하므로 1더하기)
print('생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.')
input_data = input().split()
n = int(input_data[0]) #원소의 개수
target = input_data[1] #찾고자 하는 문자열
print('앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.')
array = input().split()
#순차 탐색 수형결과 출력
print(sequentail_search(n,target,array))이진탐색알고리즘
- 이진 탐색: 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
- 이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다
이진 탐색 동작 예시
- 이미 정렬된 10개의 데이터 중에서 값이 4인 원소를 찾는 예시를 살펴보자

- [Step 1] 시작점: 0, 끝점: 9, 중간점: 4 (소수점 이하 제거)
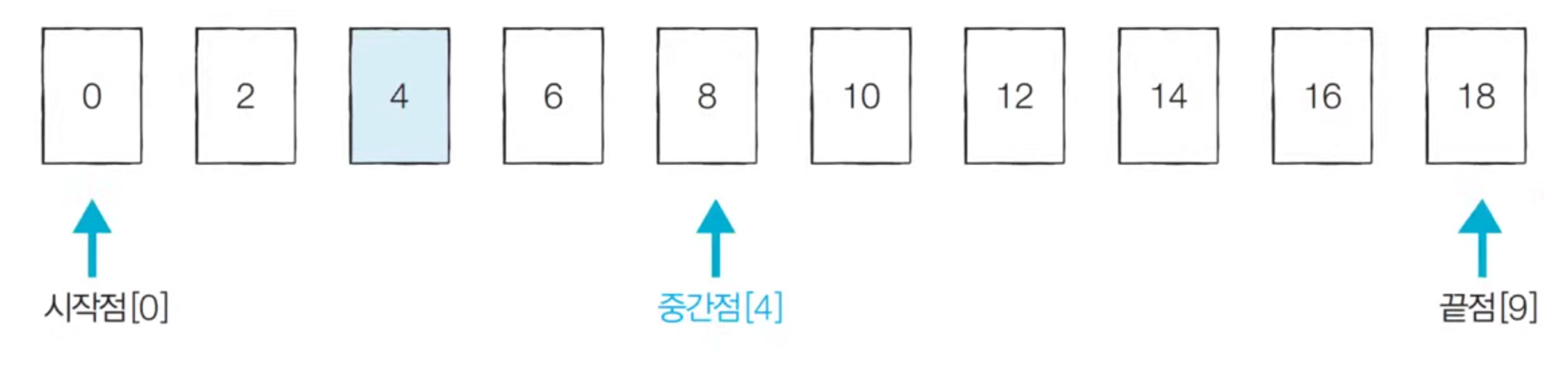
- [Step 2] 시작점:0, 끝점: 3, 중간점: 1 (소수점 이하 제거)
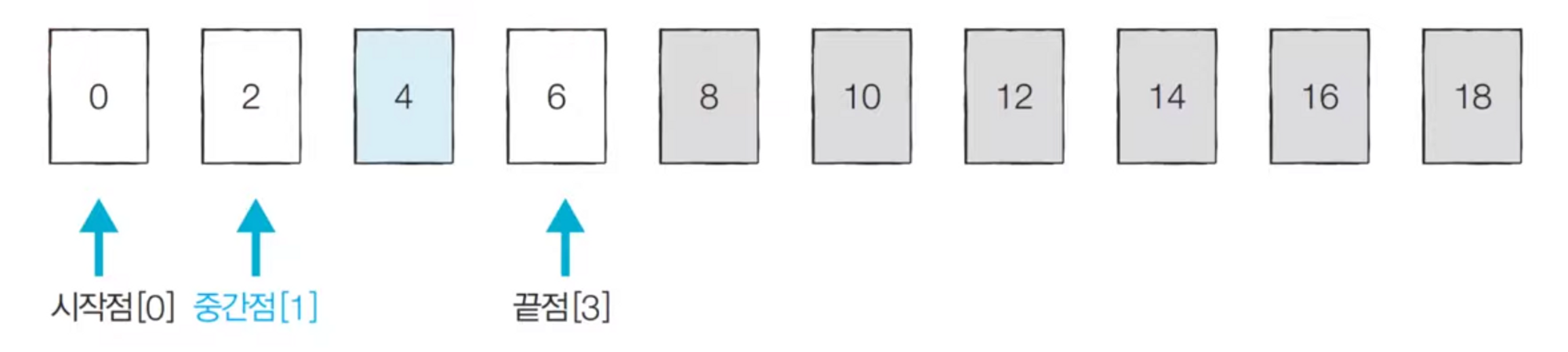
- [Step 3] 시작점: 2, 끝점: 3, 중간점: 2 (소수점 이하 제거)
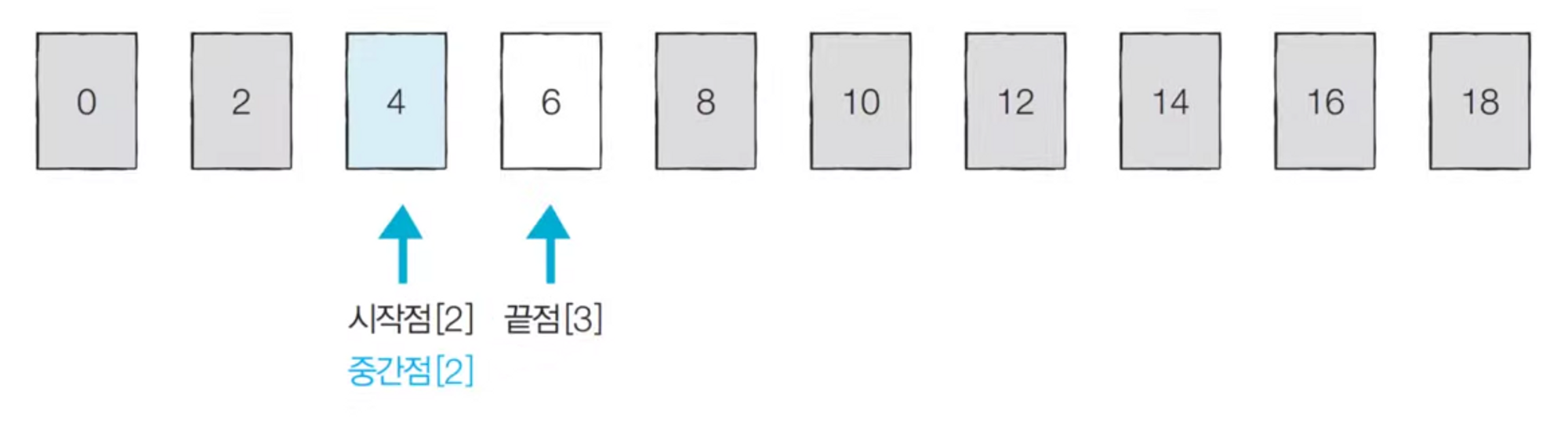
이진 탐색의 시간 복잡도
- 단계마다 탐색 범위를 2로 나누는 것과 동일하므로 연산 횟수는 log₂𝑁에 비례한다
- 예를 들어 초기 데이터 개수가 32개일 때, 이상적으로 1단계를 거치면 16개가량의 데이터만 남는다
- 2단계를 거치면 8개가량의 데이터만 남는다
- 3단계를 거치면 4개가량의 데이터만 남는다
# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid + 1, end)
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다")
else:
print(result + 1)# 이진 탐색 소스코드 구현 (반복문)
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
end = mid - 1
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
start = mid + 1
return None
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)마지막 정리
이진 탐색
- 정렬된 배열에서 중간 값을 비교하여 탐색 범위를 반씩 줄여가며 원하는 값을 찾는 알고리즘.
- 시간 복잡도는 O(log n)으로 매우 효율적이지만, 배열이 정렬되어 있어야 한다는 제약이 있다.
- 이진 탐색은 반복문 또는 재귀적으로 구현할 수 있다.
순차 탐색
- 배열이나 리스트와 같은 선형 구조에서 처음부터 끝까지 원하는 값을 찾을 때 사용하는 간단한 탐색 알고리즘.
- 시간 복잡도는 O(n)으로 배열의 크기에 비례하여 선형적으로 증가한다.
- 배열이나 리스트의 크기가 작거나 정렬되지 않은 경우에 유용하게 사용될 수 있다.
