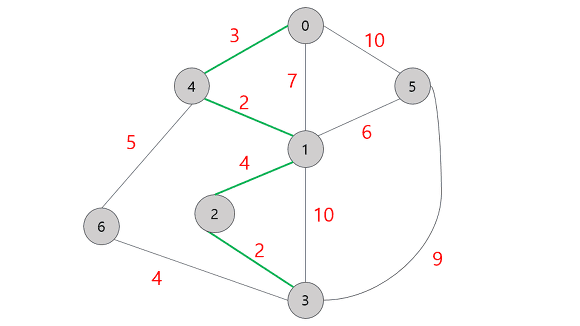
최단 경로 문제

• 최단 경로 알고리즘은 그래프에서 가장 짧은 경로를 찾는 알고리즘을 의미합니다.

• 다양한 문제 상황에서 사용될 수 있으며, 주요한 경우는 다음과 같습니다

  • 한 지점에서 다른 한 지점까지의 최단 경로
  • 한 지점에서 다른 모든 지점까지의 최단 경로
  • 모든 지점에서 다른 모든 지점까지의 최단 경로

이때, 각 지점은 그래프에서 노드로 표현되며, 지점 간 연결된 도로는 그래프에서 간선으로 표현됩니다.

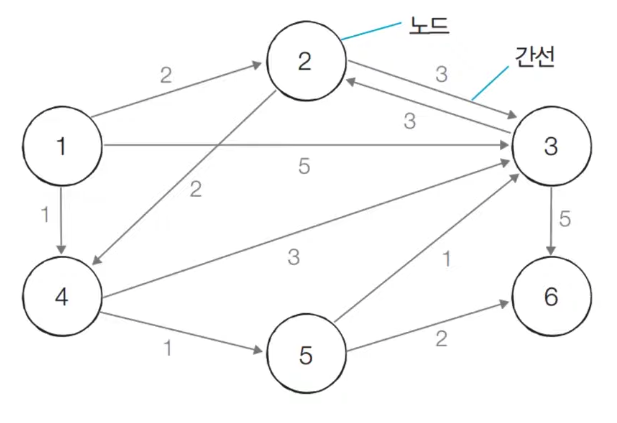
다익스트라 최단 경로 알고리즘 개요

다익스트라(Dijkstra) 최단 경로 알고리즘은 특정한 노드에서 출발하여 다른 모든 노드까지의 최단 경로를 계산하는 알고리즘입니다. 이 알고리즘은 음의 간선이 없을 때에만 정상적으로 동작하며, 그리디(Greedy) 알고리즘에 속합니다.

다익스트라 알고리즘 동작과정

[초기 상태] 그래프를 준비하고 출발 노드를 설정한다

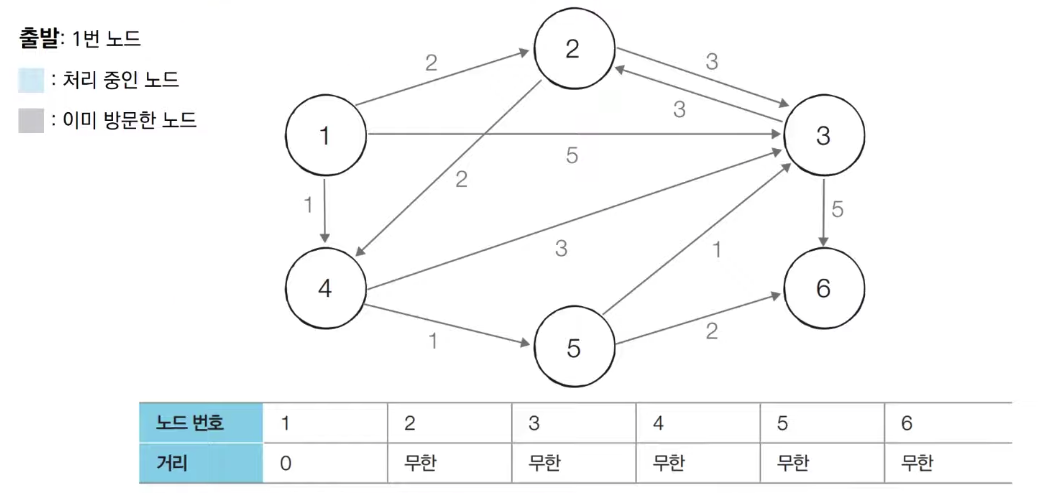
1. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 1번 노드를 처리한다
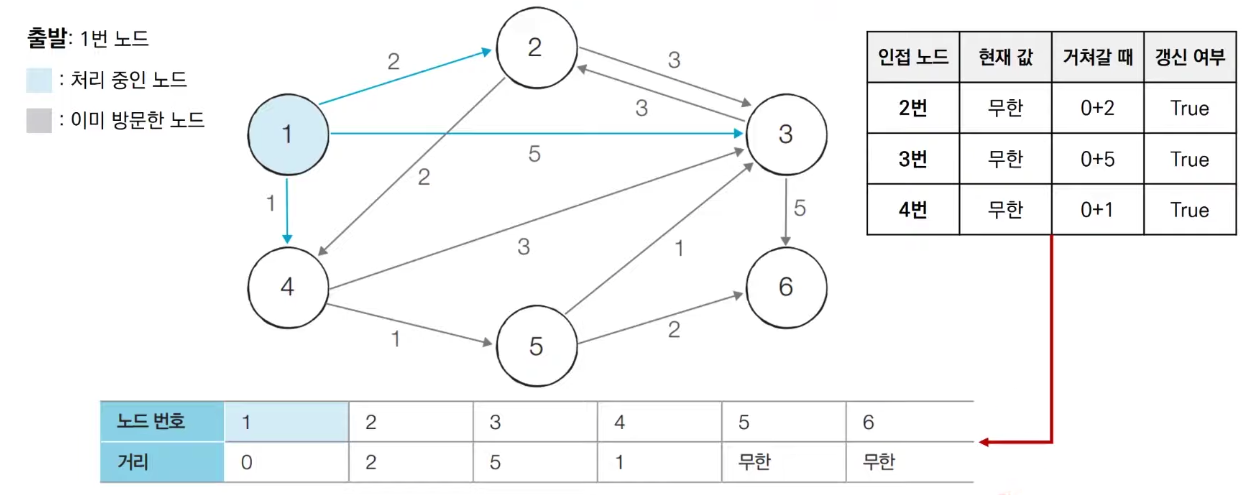
2. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 4번 노드를 처리한다
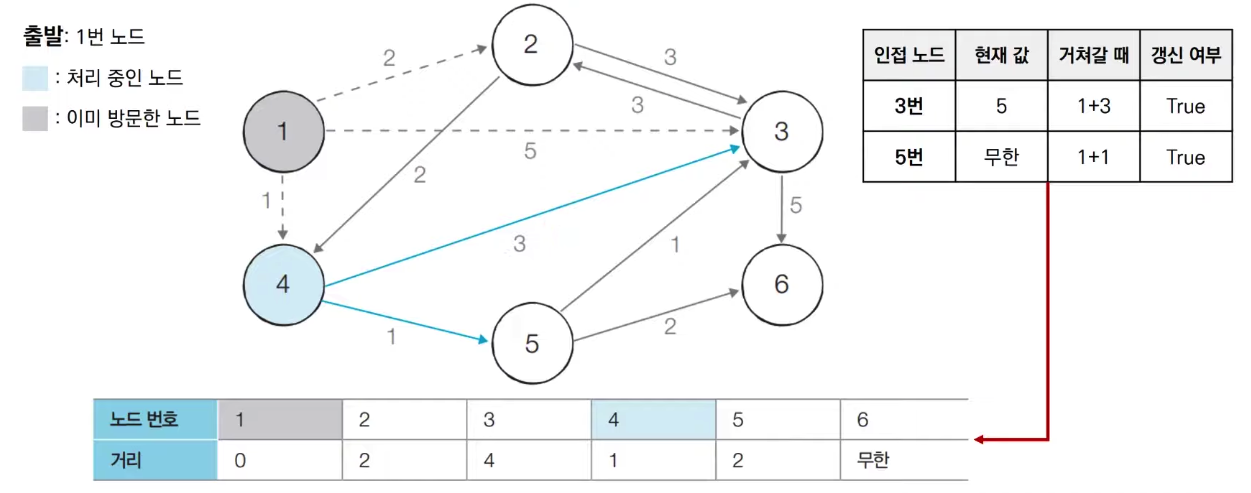
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 2번 노드를 처리한다
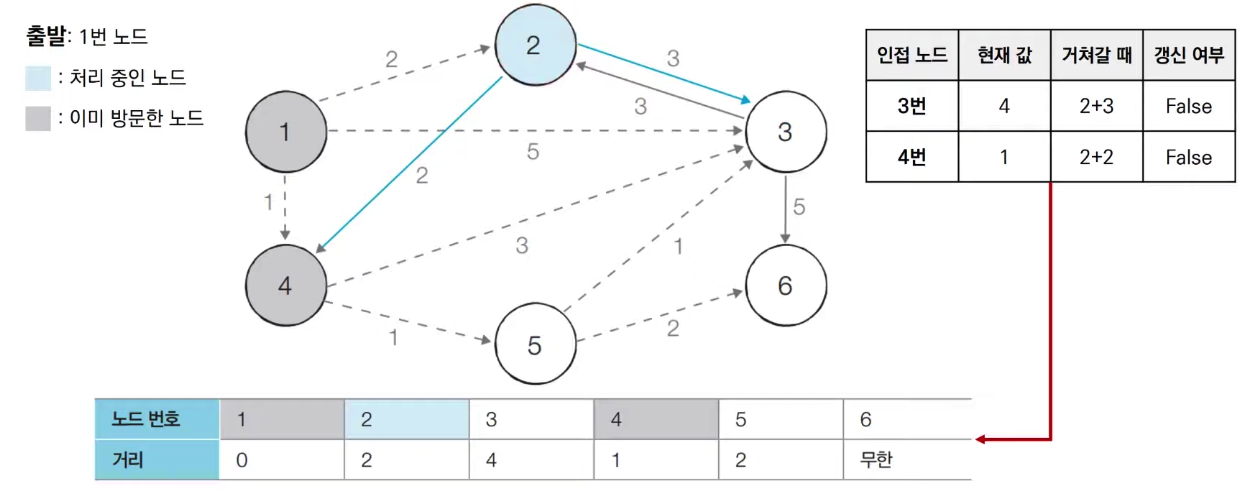
4. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 5번 노드를 처리한다
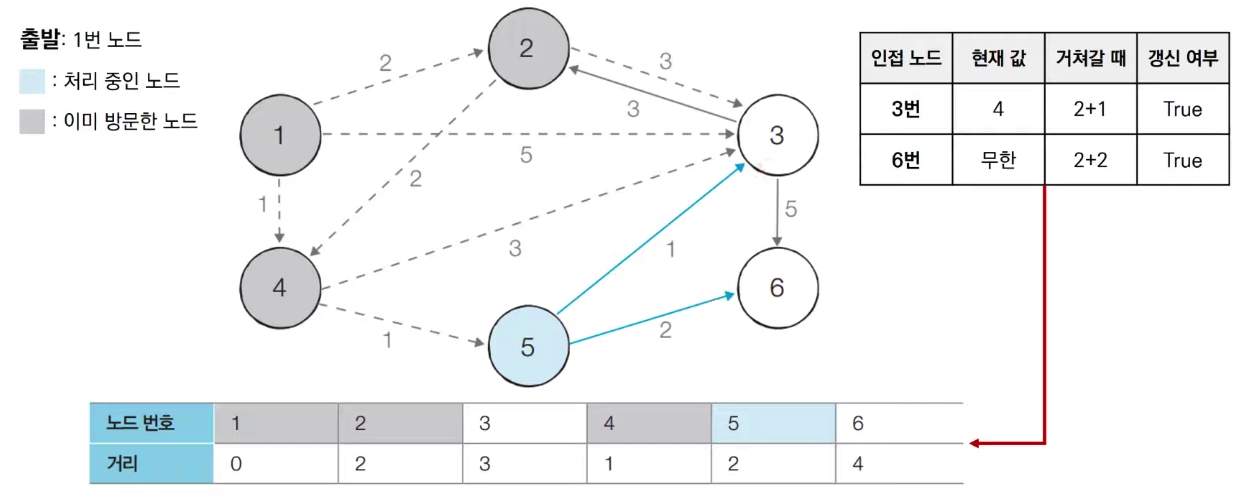
5. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 3번 노드를 처리한다
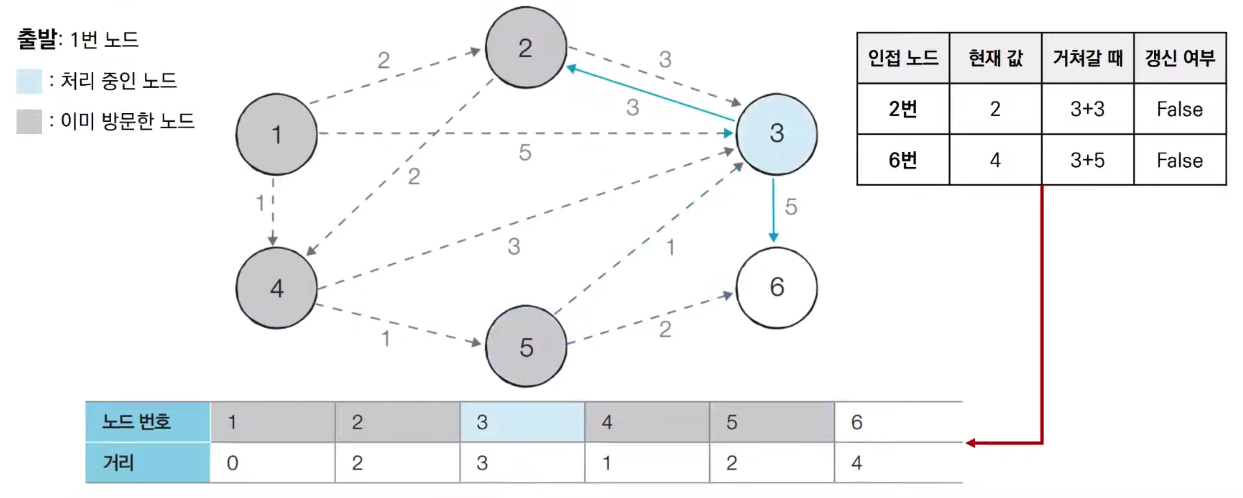
6. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 6번 노드를 처리한다

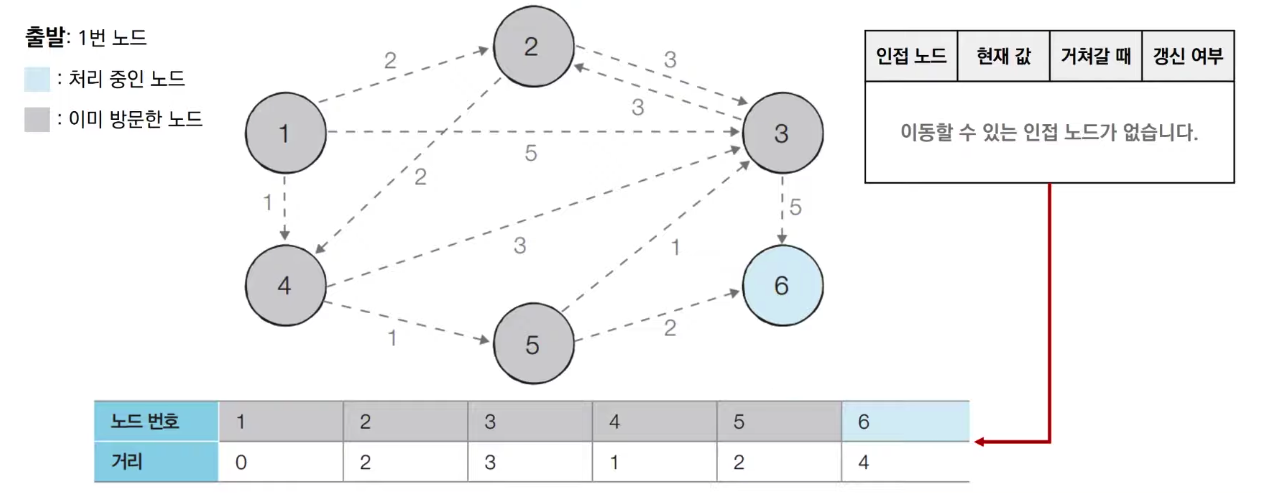
다익스트라 알고리즘의 특징

그리디 접근 방식: 다익스트라 알고리즘은 각 단계에서 방문하지 않은 노드 중에서 현재까지의 최단 거리 추정치가 가장 작은 노드를 선택합니다. 이를 통해 임의의 과정을 반복하며 최단 거리를 점진적으로 갱신해 나갑니다.

최단 거리의 확정: 알고리즘 수행 중 한 번 처리된 노드의 최단 거리는 더 이상 변경되지 않습니다. 다시 말해, 각 노드에 대한 최단 거리는 점점 정확하게 확정됩니다.

단계적 접근: 다익스트라 알고리즘은 각 단계마다 하나의 노드에 대한 최단 거리를 확실히 찾아냅니다. 이러한 접근 방식을 통해 그래프의 모든 노드에 대한 최단 거리를 구할 수 있습니다.

최단 거리 정보 저장: 알고리즘을 실행한 뒤에는 각 노드까지의 최단 거리 정보가 테이블에 저장됩니다. 이 정보를 통해 출발 노드로부터 다른 모든 노드까지의 최단 경로와 거리를 쉽게 확인할 수 있습니다.